株式会社ヘキサドライブ | HEXADRIVE

こんにちは、ナカムラです。
四色問題というものをご存じでしょうか？
現在公開中のある映画で、キーワードの１つとして説明されているので、ご存じの方もおられるとは思いますが、簡単に説明してみます。
四色問題とは、数学界の中で提示された、難解な証明問題です。
「どんな地図も、四色で塗り分けることが可能である」という命題が正しいかどうかを検証する問題なのですが、この場合の地図とは実在の地図とは限らず、架空のものも含みますので、その境界線には無限のバリエーションがあります。

実はこの命題、既に正しいことが証明されています。
ただ、その証明方法がいささか力業なので、人によっては「美しくない」と言う人もいます。

領域を分ける線（地図でいう国境線）のパターンには限りがあることを証明し（それでも１００パターン以上！）、その全てが４色で塗り分け可能であることを、コンピュータを使って全て実際に塗ってみた

という証明方法です。
「コンピュータを使って実際に全パターンを試す」
という点が、力業で美しくないと言われる要因だと思いますが、ゲームプログラミングでは似たようなこと、結構やります。
膨大な作業を繰り返すというのは、コンピュータの得意技ですからね。
例えばゲーム中頻繁に行われる当たり判定にしたって、（最も単純な方法では）総当たりによるチェックをしますから。
もっと単純に、
「数多く存在する点の内、指定した座標vに最も近い点を探す」
という処理ではどうでしょう？
指定された座標vと、全ての点との距離を計算し比較する、といういわゆる総当たりチェックでもいいと思います。
ただし、点の総数がある程度以下の数であるならば。
この方法ですと、点の総数に比例して検索時間が長くなってしまいますので、点の数が膨大な状況では、あまり得策ではありません。
点の存在する領域をある程度区分けしておき、予めどの点がどの領域に所属するのかを判定しておく。
こういう前準備を行っておけば、実際の検索に費やす時間は短く済みます。
どの領域に点が存在するのかを特定できれば、あとはその領域内の点に限定して検索すれば済みます。

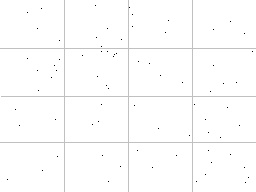
この考え方を極限まで推し進めたのが、ボロノイ図という図を用いた手法です。
点１つ１つの「縄張り」を予め計算しておくことで、領域さえ特定すれば最近点が得られるという方法です。
実際のゲームでは、ここまで厳密に縄張りを計算することは（今のところ）無いと思います。
。
http://ja.wikipedia.org/wiki/%E3%83%9C%E3%83%AD%E3%83%8E%E3%82%A4%E5%9B%B3
このボロノイ図とは、計算幾何学という学問で使われる概念です。
計算幾何学とは、図形に関する処理をコンピュータで解決する上で、最も効率的な方法を探し出す学問で、1970年代頃に生まれた比較的新しい学問です。
ハードウェアの進化と共に扱うデータ量が飛躍的に増え、またその精密さも問われる傾向が強くなってきてますから、今後のゲームプログラムには必要になってくるかもしれませんね。