株式会社ヘキサドライブ | HEXADRIVE

こんにちは、Ritaro です。

こちらに記事を書くのはこれで７回目となります。
今回も、どうぞよろしくお願い致します。

TAにとって開発上の問題点を解くのに技術的な引き出しを色々な持っておくことが必要、
について・・また少し紹介したいと思います。

前回の記事内容

TA と Maya Node Editor その３

に引き続き、Mayaの Node Editorまわりの話、その４です。

キャラクターセットアップ等に便利に使える手段の１つです。
コンストレイント＞作成下にあるペアレントやポイントといった
機能以外にも制御する方法があるということで、
今回も　ノードの組み合わせでオブジェクトをワールド座標値で設定する方法や
更にベクター(Vector)についても話をしてみようと思います。

では、さっそく・・

ちょっと具体的な、面白い対処法、でもあったら『おお、使えるかも』
・・って思うようなものをまたご紹介していきましょう。

４）「Maya NodeEditor を使った　ワールド座標のベクター」その２

さー vectorProductノードを使ってより本格的な計算例をご紹介しよう
と思いましたところで終わってしまいました。

その時はやったことは、
ベクターのノーマライズ　を行うのに
plusMinusAverage の操作　減算　の後、
distanceBetween の距離 と multiplyDivide の操作　除算で
求めるのではなく、
plusMinusAverage の操作　減算　の後、
vectorProduct 操作を　ベクトル行列積 に、
そして　[レ] 出力の正規化　にチェックを入れて有効にするだけで
求めるられる、というところでした。(前記事チェックしてください)

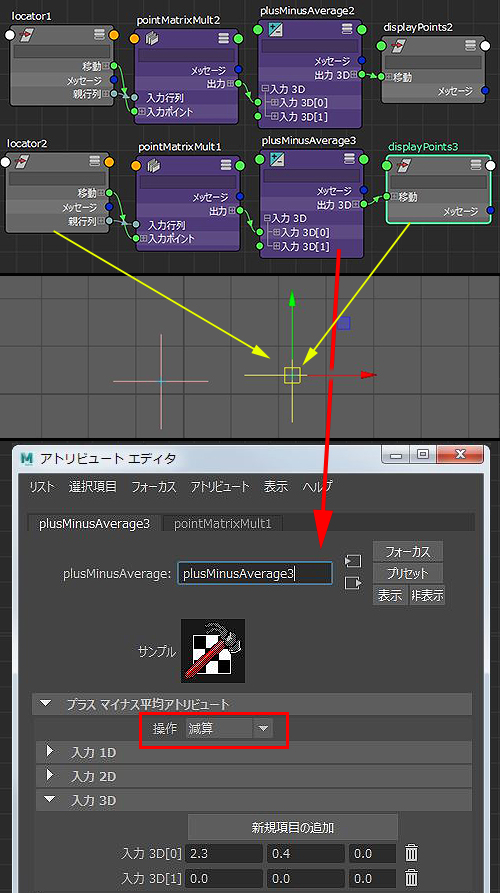
では、２つの locator のグローバルの位置は　pointMatrixMult　についないだ
親行列と移動　値から得るとして
それをベクター値にするには　plusMinusAverage　の　3dD[0] 入力し
操作を　減算　にしたものと　とします。

試しに　一旦　displayPoints　というノードを繋げると
位置が一致することが目で見て確認出来ます。

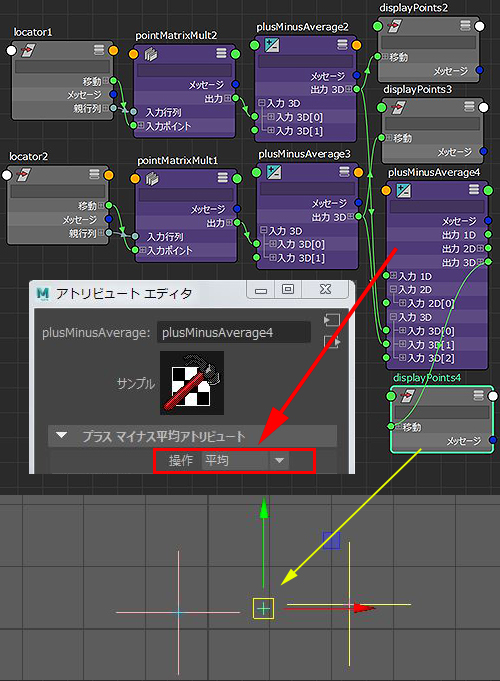
これで　２つベクターが得られたので、
２つのベクターを　plusMinusAverage　で操作を再び　平均とすれば
２点間の中間が　ベクターから計算出来たことになります。

 

　■ 外積 (Cross Product)

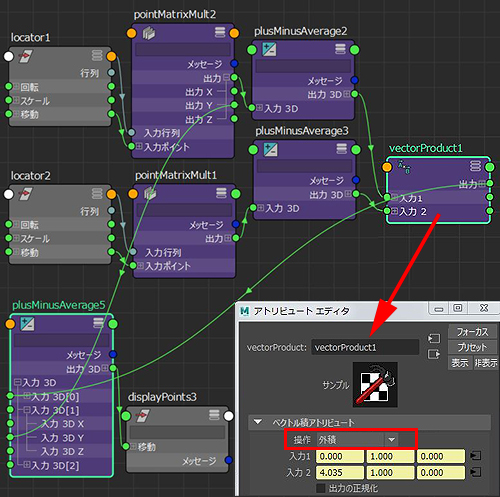
そうしたら、２つのベクター値を　vectorProduct　につなぎ
操作を　外積　にして何が得られるか目で見てみましょう。

locator1　の位置は　0.000　1.000　0.000　としました。
locator2　の位置は　4.000　1.000　0.000　としました。

vectorProduct　へのつなぎ方は
１つのLocatorから得た２つベクターを
それぞれ　入力１　と　入力２　につなぎ
vectorProduct　の操作は　外積　とします。

この状態をMayaのシーンを上から見ると
locator2　を左右（X軸方向）に動かすと
displayPoints3　はその同じ分を直角上下(Z軸方向)に動きます。

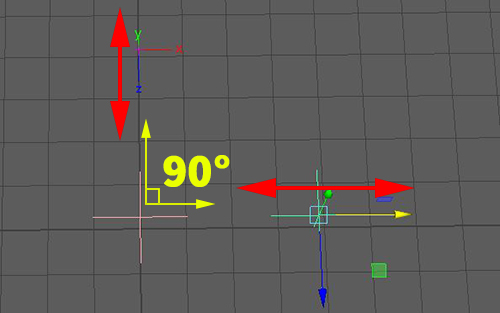
locator2　を上下（Z軸方向）に動かすと
displayPoints3　　はその同じ分を直角左右(X軸方向)に動きます。

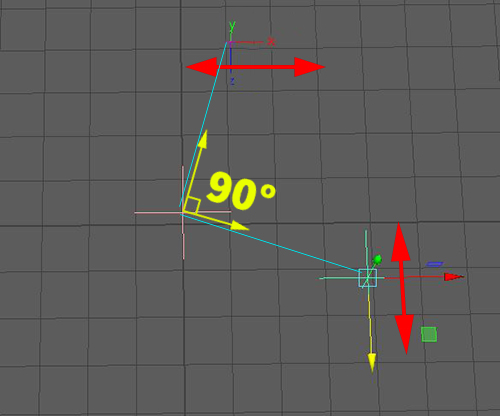
つまり、locator1を中心にlocator2の方向(ベクトル)に対して
直角(90度)を保った位置(displayPoints3)　を算出している
という結果を目で見えるかたちで示しています。

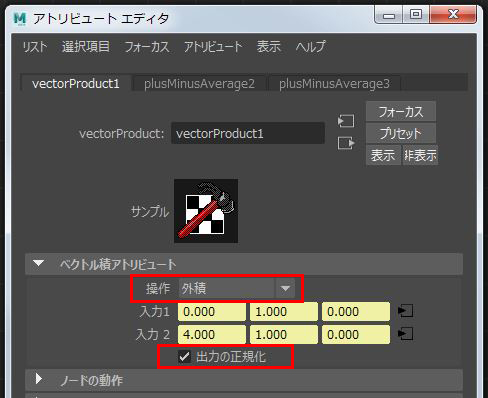
ただし、位置の動きが大きい値で変化してしまうので、
通常は　vectorProduct　の　操作は　外積　の下の
[レ]　出力の正規化　にチェックと入れて有効化し、
ノーマライズ（0から１の値）にして利用します。

 

　■ 内積 (Dot Product)

今度は、２つのベクター値を　vectorProduct　につなぎ
操作を　内積　にして何が得られるか目で見てみましょう。

locator1　の位置は　0.000　1.000　0.000　としました。
locator2　の位置も　0.000　1.000　0.000　としました。

結果が見える　displayPoints4　には
内積から得た値が　移動X　に入るようにしてあります。

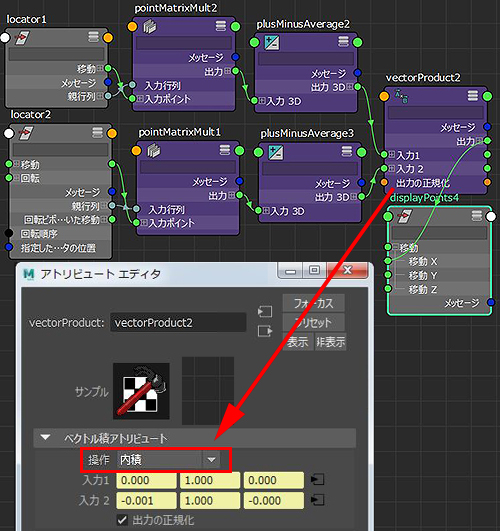
解りやすいように　locator2　は　半径1.0 の円カーブ上に
パスコンストレイント　してあります。
フレームを0から120にすると時計まわりに回るようにしてあります。

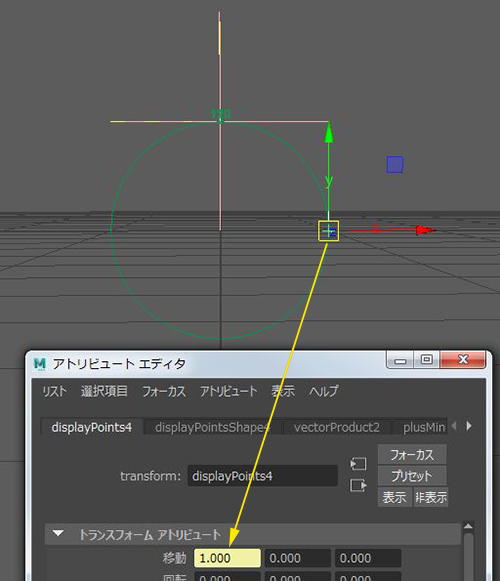
locator1 と　locator2　のベクトルが同じ向きだと
内積の結果は　1.0　になります。

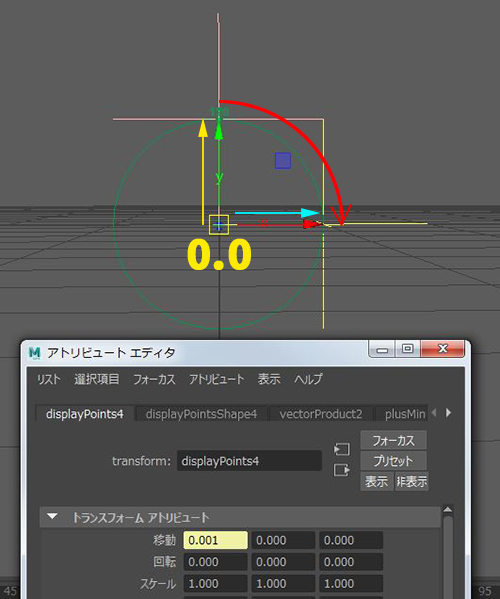
locator1 と　locator2　のベクトルが90度の向きだと
内積の結果は　0.0　になります。

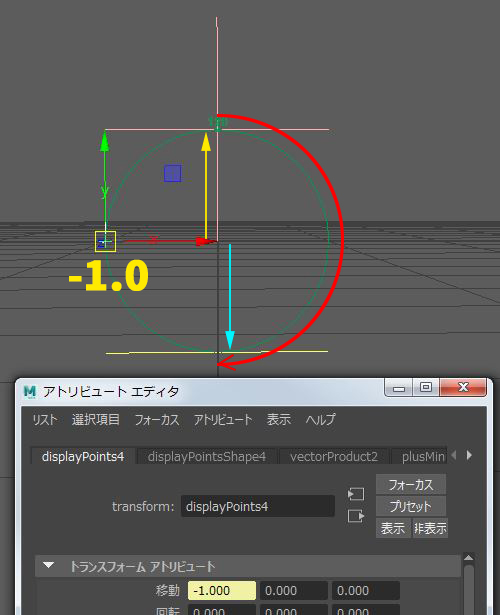
locator1 と　locator2　のベクトルが逆向きだと
内積の結果は　-1.0　になります。

この内積の結果を最も良く使うのがシェーダーになります。
locator1　が　平行光源のベクトル
locator2　が　オブジェクトの法線の向きに置き換えて考えます。
もっとも明るい部分は
光のベクトルと法線が同じ向きの場合であり
一番暗い所は　光が当たらない　つまり　逆向きの
黒（0.0以下の値は0.0の黒と考える）になります。

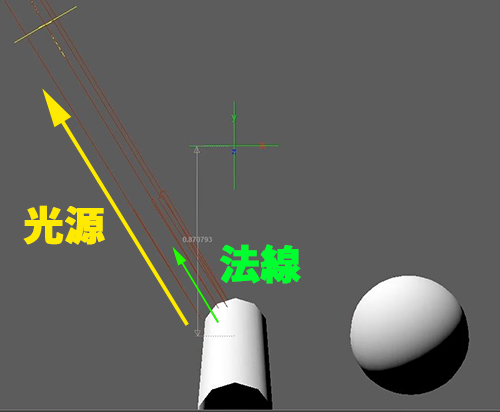
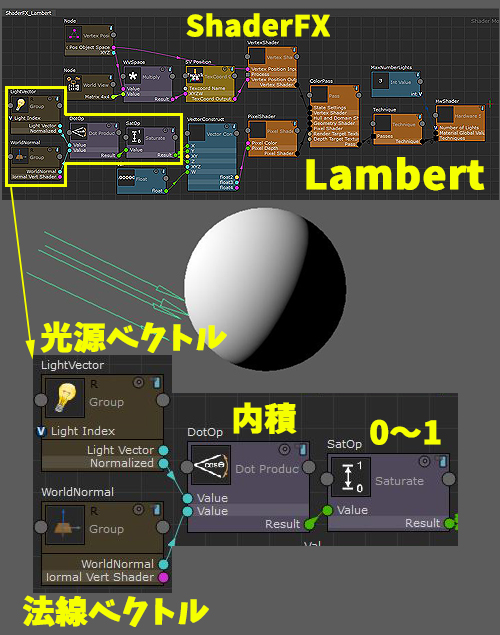
下図はMaya/Maxに搭載されているリアルタイムシェーダーである
ShaderFXの説明の時に利用したシーンの画面ですが、
一番明るい所が光源ベクトルと法線ベクトルの向きが一致
している場合という説明になります。

ここでの話しは少し横道にずれますが、
ついでにShaderFXでの内積を使った光源処理も見てみましょう。
いわゆるランバート(Lambert)を表現する為の描画結果を
得る為に　光源とオブジェクトのワールドの法線の
ベクトルを内積を使って導き出していることが
理解できると思います。

といったところで、今回はここまで。

また次回も、NodeEditor　についての続きが出来たらと思っております。

ではでは。

*—–
Ritaro