株式会社ヘキサドライブ | HEXADRIVE

GCコン（スマブラブラック）が家に届いて、
「今って西暦何年だっけ？」と一瞬冷静になったプログラマの某（なにがし）です。
FFCCもリマスターされるし、GBAをSwitchに繋ぎたくなってきました。

さて、これまでのブログ記事で、画像のリサイズ手法を紹介してきました。

【ニアレストネイバー編】
【バイリニア編】

次はバイキュービック法かなと思いつつ実装してないので、実開発で使ったLanczosを話します。
理論がややこしいので、まずは乱暴なイメージ優先で説明します。

バイリニア法やバイキュービック法は、着目点の周辺ピクセルを一定数抜き出し、
着目点との距離に基づく補間をする、と解釈できます。参照するピクセル位置が飛び飛び。

範囲内の全ピクセルを参照して補間できれば、より高精度になるような気がします。

そこで「窓関数」を使います。一定範囲外を重みゼロとするような関数です。
窓関数にも色々ありますが、画像の拡縮についてはLanczos窓が有効だと言われます。

正の整数Nに対して、Lanczos窓L(x)は次のように定義されます。

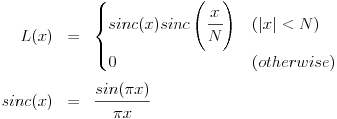
sinc関数はx = 0のとき、分子と分母がともにゼロとなりますが、極限をとると1になります。
なので、ゼロ除算回避のため、0が与えられたときに1を返すよう実装しておくと安心です。

画像の拡縮としては、N=2でそれなり、N=3で十分に高精度だと言われます。
N=4以上は処理負荷的にしんどい。。。

N=3のとき、3次Lanczosだとか、Lanczos-3だとか呼ぶようです。グラフ化したのが下図。

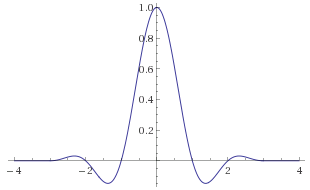
Lanczosの引数として画像上の距離を与えるとすると、
定数Nは、「着目点から周辺何ピクセルを見るのか」という意味になります。

例えば、Lanczos-3なら距離3未満のピクセルを見ていきます。
その範囲外はゼロとして定義したので、計算不要なのです。

では、実装を示します。

1ピクセルを決めるにあたって、周辺ピクセルに重みをかけて足し合わせていますが、
重みは影響の強さを定義しているだけなので、足しただけでは色としては不正な値をとります。
重みの合計が1となるよう調整すればよいので、重みの合計値で最後に割ってます。

また、途中で同じ計算結果が何度も出てくるので、ある程度は使い回す最適化もしています。

比較画像を示します。
弊社「魔法パスワード1111」のトルネードちゃんです。

↑1.5倍

↑オリジナル

↑0.5倍

縮小めっちゃきれいじゃないですか？？

手始めにバイリニアを実装したときは
「ダメダメダメ、トルネードちゃんはもっとかわいいんだよ！」と思いましたが、
Lanczos-3で「やったー！かわいい！」という出来になって安心しました。

ただ、処理は重めです。

Lanczos-3では、距離3未満、つまり、1辺の長さ6の正方形の内側を考慮に入れて、
初めて目的画像の1ピクセルが決まります。

これを2次元に適用するので、
少なくとも((3 – 1) * 2 + 1 )^2 = 5^2 = 25ピクセル見ることになります。
ここで-1が出てきたのは、距離3「未満」という境界条件により両端が除外されるため。
また、+1は距離0つまり中心点の考慮によります。

さらに縮小を考えると、参照ピクセル数が一気に増えます。
例えば、0.5倍スケールだとすると、目的画像の1ピクセルを決めるためには、
((3 / 0.5 – 1) * 2 + 1)^2 = 11^2 = 121ピクセルを見ることになります。
間引いて最低限必要な25ピクセルだけでも計算できますが、ここでは全部やるということで。

きれいになればよかろうなのだと思っていたものの、並列化してやっと気軽に使える感じです。
これより劇的に高速化したいなら、マネージドコードを諦めた方が良さそう。

最後に、Lanczos窓を選ぶ理論的背景をざっくり説明します。
※わかる人向けの駆け足説明であり、正確でないことはご容赦ください（予防線）。

＝＝むずかしいはなしはじまり＝＝

画像は2次元空間をピクセル単位でサンプリングした「輝度の離散信号」であるとみなせます。
これを補間して連続信号に変換できれば、一定間隔で再サンプリングするのがリサイズです。

サンプリング定理を満たすとき、周波数領域において
サンプリング周波数の半分（ナイキスト周波数）以下が復元したい連続信号に相当します。

これを愚直に計算するなら、「離散信号をフーリエ変換」して、「周波数フィルタ」を通し、
「逆フーリエ変換で連続信号に戻す」という手順になります。実際はもっとシンプルにできます。

フーリエ変換の特性によって、周波数領域でフィルタ関数と積を取ることは、
フィルタ関数を逆フーリエ変換したものを、離散信号に対して畳み込み積分することと等価です。

畳み込み積分とは、着目点の周辺も重み付けにより考慮に入れることであり、
離散信号であれば重みをかけた値をひたすら足すことです。実装が簡単で処理効率も良い。

あとは逆フーリエ変換済みのフィルタ関数が決まればいいですね。
特定周波数以下だけ通過させる理想的なローパスフィルタを逆フーリエ変換するとsinc関数になります。

しかし、sinc関数そのままでは無限の範囲を扱うことになり計算不可能です。
有限範囲で定義された窓関数で妥協する必要があり、sincに似た性質を持つ窓であるLanczosを使います。

ここまでは単純な補間の話ですが、リサイズであればサンプリング周波数を変えることになります。
サンプリング周波数がナイキスト周波数を下回るとエイリアシングという誤差を生じますが、
縮小時のサンプリング周波数に合わせてフィルタすれば再現不能な高周波をカットすることにもなります。

＝＝むずかしいはなしおわり＝＝

拡大も縮小も同じ理論なのでまとめて説明してきましたが、どうしても拡大はぼやけるので、
大きな原画像を用意して、用途に合わせて縮小する目的でしか利用していません。

以上で、リサイズに関する連載はひとまず終了です。
気が向いたら、バイキュービック法や面積平均法を説明するかもしれませんが、実装予定はないです。